Qwen2-Math

Qwen2-Math is a specialized large language model (LLM) focused on mathematical reasoning. Part of the Qwen2 model family from Alibaba, Qwen2-Math was introduced in mid-2024 as a series of math-specific models based on the Qwen2 architecture.

It comes in multiple sizes (approximately 1.5B, 7B, and 72B parameters) with both base and instruction-tuned variants. The base models are pretrained on general and math data, while the Instruct versions are fine-tuned for conversational and step-by-step problem solving.

Notably, Qwen2-Math significantly outperforms prior open-source models on math benchmarks and even rivals some closed-source systems in mathematical tasks. The model is released under an open-source Apache 2.0 license, making it accessible for developers to integrate into their applications.

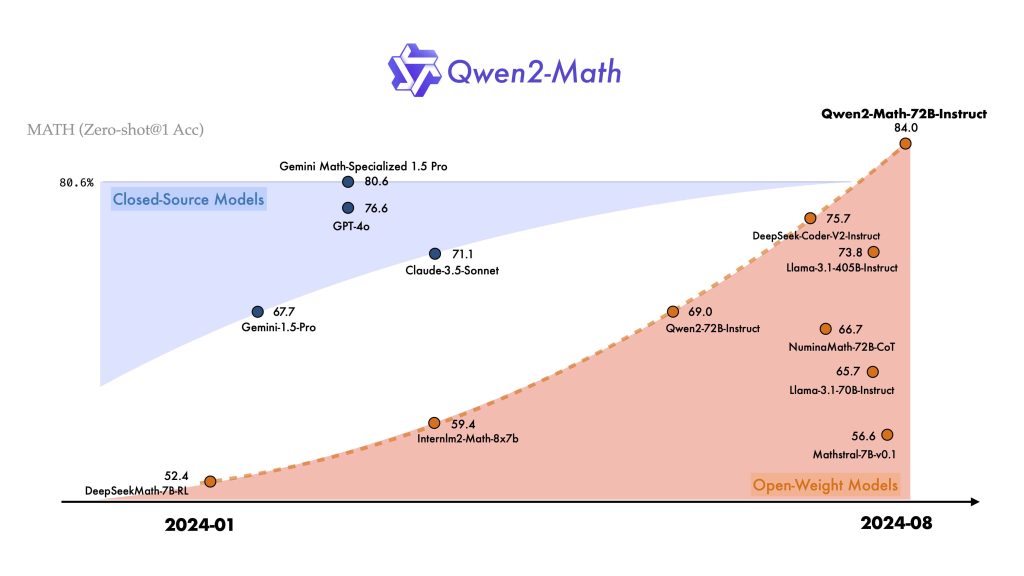
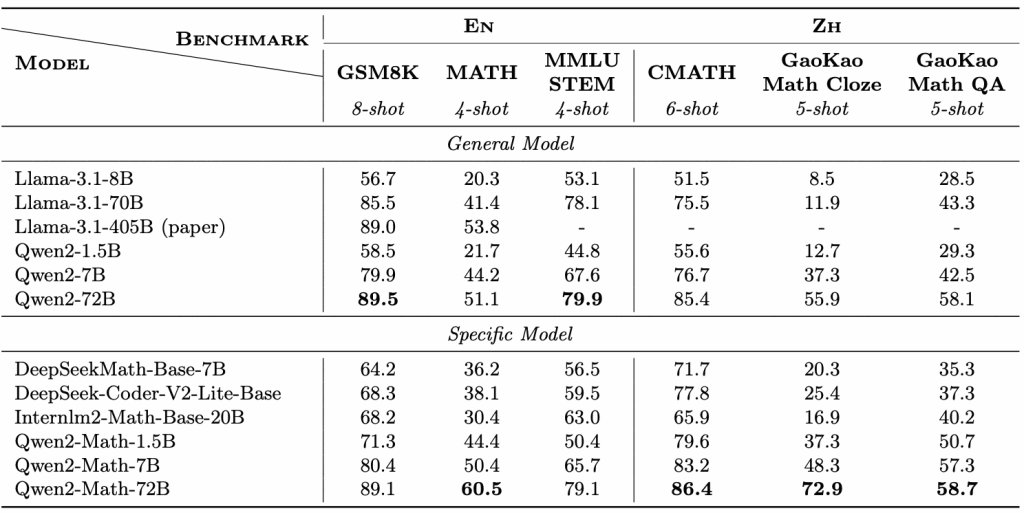
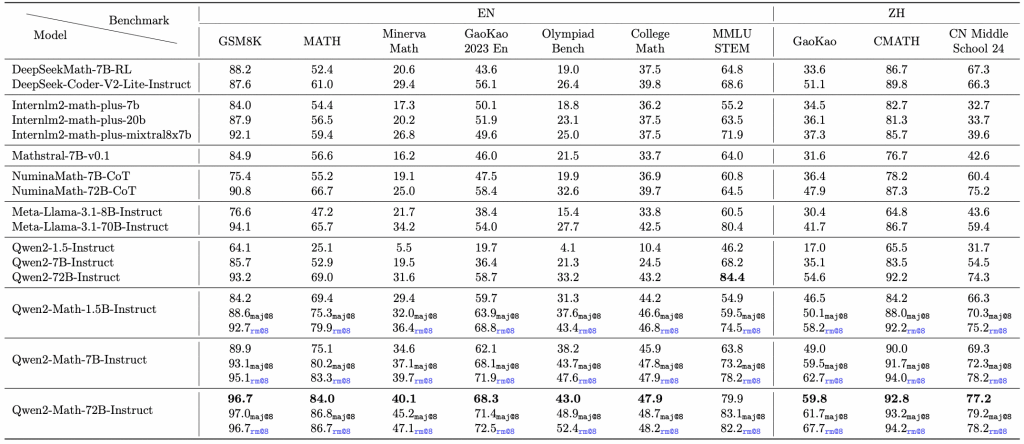
Qwen2-Math is designed to tackle complex, multi-step mathematical problems with a high degree of reasoning. Its development was driven by the need for LLMs that can understand and solve math tasks – from basic algebra to competition-level problems – more reliably than general-purpose models.

Over the course of development, the Qwen team prioritized improving arithmetic accuracy, logical consistency, and the ability to carry out symbolic reasoning steps. The result is a model that can serve as a math problem-solving engine, capable of showing its work and producing well-formatted solutions.

Architecture and Math-Focused Training

Foundation Architecture: Qwen2-Math builds upon the Qwen2 LLM architecture, which is a Transformer-based decoder-only model. Qwen2 introduced several architectural enhancements beneficial for math reasoning, including Grouped Query Attention (GQA) and Rotary Positional Embeddings (RoPE) for efficient long-context handling. All Qwen2 models (from 0.5B up to 72B parameters) use GQA to reduce memory usage and improve inference speed.

They also support extended context lengths: Qwen2’s larger models can handle inputs up to 128K tokens in the instruction-tuned versions. This means Qwen2-Math inherits the ability to process lengthy mathematical derivations or large problem statements without losing track of context. The 7B and 72B Qwen2-Math-Instruct models, for example, can utilize extremely long prompts (tens of thousands of tokens) when needed, which is valuable for complex proofs or multi-part problems.

Model Variants: As noted, Qwen2-Math is available in roughly three parameter scales – 1.5B, 7B, and 72B – each as a base model and an instruction-tuned model. The base models are pretrained on vast corpora and suitable for direct prompting or as a starting point for further fine-tuning. The Instruct models (Qwen2-Math-7B-Instruct) have undergone supervised fine-tuning and alignment, making them better at following prompts and producing step-by-step answers out-of-the-box. In practice, developers will use the instruct models for most applications, since they are optimized for conversational Q&A and complex reasoning, whereas the base models are used for completion tasks or custom training.

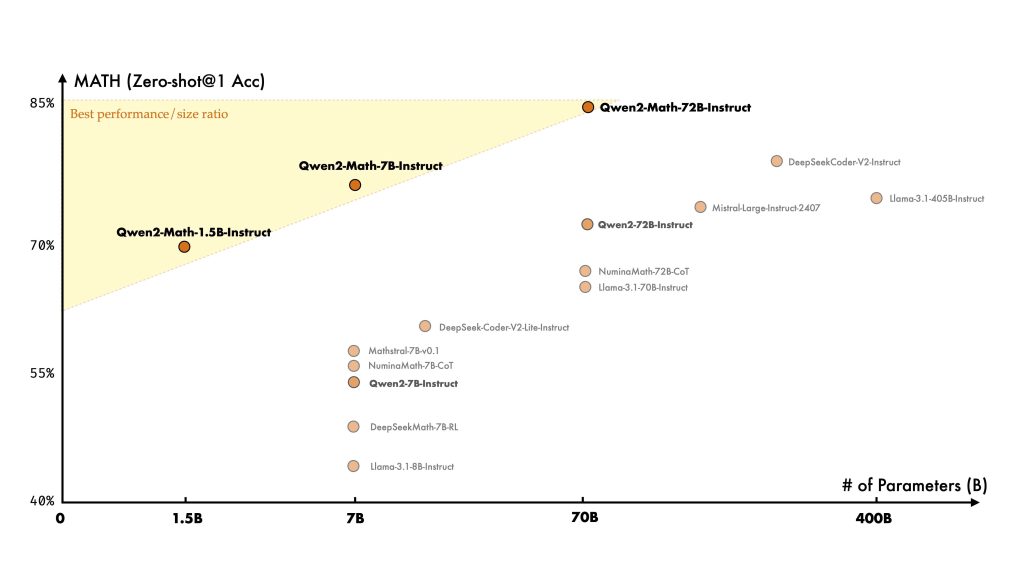
Mathematics-Enhanced Pretraining: A crucial aspect of Qwen2-Math is its specialized training data. The base model initialization starts from the general Qwen2 LLM (trained on diverse text in many languages) and is then pretrained on a Mathematics-specific corpus. This corpus was meticulously curated to include large-scale, high-quality math content: web pages and articles with mathematical discussions, digital textbooks and academic papers (likely containing formulas and proofs), source code (useful for algorithmic thinking and tool use), and collections of exam problems and solutions. Additionally, a portion of the training data was synthetic math data generated by Qwen2 itself. By synthesizing math problems and solutions, the developers augmented the training with rich examples beyond what human-curated datasets provide. This upsampling of mathematical content ensures the model has seen a wide variety of mathematical expressions and problem types.

Instruction Tuning with Math Reasoning: After pretraining, the Qwen2-Math Instruct models were further refined using human-aligned fine-tuning and reinforcement learning, specifically tailored for math problem solving. The team first trained a math-specific reward model to judge the quality of answers (with signals for correctness and reasoning soundness). They then performed Supervised Fine-Tuning (SFT) on a dataset of question-answer pairs, using rejection sampling guided by the reward model to pick responses that show correct reasoning. Finally, they applied a reinforcement learning step (using a method called Grouped Relative Policy Optimization, GRPO) to fine-tune the model to optimize the reward further. This pipeline encourages the model to produce accurate and well-reasoned solutions, not just any plausible text. In essence, Qwen2-Math was taught to “show its work” and arrive at correct answers through a combination of supervised examples and reward-driven adjustments. The result is improved reasoning stability and accuracy, without us naming any specific competing model.

It’s worth noting that the largest model (72B) was used to generate additional training data and rewards for the smaller models – a form of knowledge distillation or self-improvement used in the Qwen2.5 iteration. All this means Qwen2-Math-Instruct is highly optimized for math tasks relative to vanilla LLMs. However, because of this specialization, the Qwen team advises that the math-focused models are not ideal for general-purpose tasks outside of math; they explicitly do not recommend using Qwen2-Math for non-math domains. The model may lack the broad knowledge or conversational finesse of a generic LLM, as some capacity was redirected toward math expertise.

Supported Input Formats for Math Prompts

One of the strengths of Qwen2-Math is its ability to understand and generate mathematical notation and structured expressions in prompts:

• Plain Language Text: You can feed Qwen2-Math natural language problems just as you would to any LLM. For example, “If one angle of a triangle is 30 degrees and another is 60 degrees, what is the third angle?” would be perfectly understood. The model parses the text and identifies the mathematical relationships described.
• LaTeX and Formulas: Qwen2-Math was trained on a large amount of data containing LaTeX math formulas and scientific notation. Its tokenizer and vocabulary are math-aware, meaning it can handle specialized tokens (like $ \frac{ }{ } $, \int, ^, subscripts, etc.) without breaking them in odd ways. This allows you to include properly formatted equations in your prompts. For instance: “Solve the equation $e^{2x} = 5$ for $x$.” The model will interpret the LaTeX expression $e^{2x}=5$ correctly. Math-specific tokenization helps it precisely represent symbolic expressions and even produce well-formed LaTeX in its output. Multi-line or complex formulas (such as matrices or piecewise definitions) are also supported to the extent the context size allows.
• Math Expressions & Code: Beyond pure LaTeX, Qwen2-Math can accept pseudo-code or arithmetic expressions directly. You could prompt it with something like: “Calculate 2 * (3.14159^2) / 0.5” or even include a short snippet of code or pseudo-code describing a math procedure. Since the training data included programming and algorithmic content, the model is familiar with reading code-like syntax. In the upgraded Qwen2.5-Math, there is explicit support for Tool-Integrated Reasoning (TIR) where the model can output and reason about Python code, but even the base Qwen2-Math can interpret many algorithmic descriptions in text form due to its coding background.

In summary, you can freely mix natural language with mathematical notation in the input. For example, a prompt could be:

“A projectile’s height is given by $h(t) = -5t^2 + 20t + 100$. What is the maximum height, and at what time does it occur?”

The model will parse both the textual question and the quadratic function provided in math notation. This flexibility in input format makes Qwen2-Math suitable for a range of sources – from plain word problems to snippets taken from textbooks or scientific documents. It’s always good practice to ensure LaTeX is properly enclosed in $...$ or $$...$$ as needed, so the model recognizes it as math and not prose. Because Qwen2-Math supports LaTeX natively, it can also produce nicely formatted equations in its answers, as we’ll discuss later.

Core Mathematical Capabilities

Qwen2-Math excels in various areas of mathematical reasoning and problem solving. Below are its core capabilities, which make it a powerful engine for developers building math-aware applications:

• Symbolic Math Reasoning: The model can manipulate symbols and expressions, not just plug numbers. This includes simplifying algebraic expressions, factoring, expanding, and doing symbolic substitutions. For example, Qwen2-Math can take an expression like x2−1x−1\frac{x^2 – 1}{x – 1}x−1×2−1​ and recognize how to simplify it (in this case, to x+1x+1x+1, with the caveat x≠1x\neq 1x=1). It handles algebraic identities and can often carry out algebraic derivations in a step-by-step manner in its responses. This symbolic reasoning extends to calculus (differentiating or integrating expressions symbolically) and other domains where manipulation of formulas is required.
• Equation Solving (Algebra and Beyond): Solving for unknowns in equations is a fundamental skill of Qwen2-Math. It can solve linear equations, systems of equations, quadratic equations, and even higher-degree polynomials or systems (to the extent analytic solutions exist or can be reasoned). For instance, if asked to “Find the value of xxx that satisfies 4x+5=6x+74x+5 = 6x+74x+5=6x+7”, the model will isolate xxx and determine the solution (in this case, x=−1x = -1x=−1), usually explaining each step (subtracting 4x, etc.). It also tackles equations in more advanced math – like solving for xxx in a trigonometric equation, or solving a system of linear equations. However, for extremely complex equations (e.g., a 5th-degree polynomial or equations requiring iterative numerical methods), it may struggle or resort to approximation, as pure chain-of-thought has limits in precise computation. Still, for a wide range of algebraic problems, Qwen2-Math provides a reliable step-by-step solution process.
• Mathematical Word Problems: Qwen2-Math is adept at understanding word problems described in plain language, which often involve translating text into mathematical operations. It handles problems from basic arithmetic word problems (rate-time-distance, age puzzles, combinatorics in story form) up to competition math word problems. The model parses the narrative, identifies relevant quantities, sets up equations or logical conditions, and works through to an answer. Its training on datasets like GSM8K (grade school math) and others has tuned it for such tasks. For example, a prompt like: “Alice has twice as many apples as Bob. Together they have 12 apples. How many apples does Alice have?” will lead the model to form equations (say A=2BA = 2BA=2B and A+B=12A+B=12A+B=12), solve for AAA and BBB, and provide the answer with reasoning. It can manage multi-step reasoning like this thanks to chain-of-thought training, often yielding an explanation that mirrors how a human would break down the problem.
• Logical & Scientific Reasoning: Beyond pure math, Qwen2-Math’s capabilities extend into logical reasoning and quantitative scientific problems. It was evaluated on STEM portions of benchmarks like MMLU, which include physics, chemistry, and other sciences. The model can analyze logical puzzles or scientific questions that require math. For instance, it can work through a physics problem by applying formulas and reasoning about the steps (e.g., computing forces, energy, using appropriate units). Its logical reasoning is strong due to the focus on step-by-step thinking – it can handle if-then scenarios, combinatorial logic, or parity arguments in number theory. In fact, the developers note that Qwen2-Math learned to generate deep step-by-step explanations covering advanced domains such as combinatorics, number theory, algebra, and geometry. This means it doesn’t just output the answer; it often explains the reasoning path, which is crucial in fields like geometry proof or combinatorial arguments where logical steps must be articulated.
• Step-by-Step Chain-of-Thought Solutions: A hallmark of Qwen2-Math’s responses is its use of chain-of-thought (CoT) reasoning. The model is explicitly trained and encouraged to produce solutions that break the problem down into intermediate steps. Instead of jumping to a final answer, it will usually outline the approach: list given information, derive intermediate results, and gradually reach the conclusion. For example, when solving an equation, it will show each algebraic manipulation on a new line. When tackling a word problem, it may enumerate known variables and equations before solving them. This chain-of-thought ability makes Qwen2-Math’s output interpretible and verifiable. Developers can even prompt the model to “show your reasoning step by step” if they want to ensure it provides the full solution path. In evaluations, using few-shot chain-of-thought prompting was key to unlocking the model’s best performance. Essentially, Qwen2-Math is built to think out loud, which is invaluable for understanding how it arrived at an answer and for debugging or verifying those answers in a critical application.
• LaTeX Rendering and Structured Output: Thanks to math-aware tokenization and training on scientific text, Qwen2-Math can produce neatly formatted mathematical output. It will often answer with equations enclosed in $...$ for inline math or in a LaTeX display format if the answer involves a formula. For instance, if asked to compute an integral symbolically, it might respond: “The integral is $\frac{1}{3}x^3 + C$.” This output is readily renderable in a front-end that supports LaTeX (such as a Jupyter notebook or a web app). It can also create lists or bullet points for multi-part answers and label different parts of the solution (e.g., “Solution: … Answer: …”). In the case of multi-step derivations, it often writes out each formula on a new line with proper alignment or reasoning text in between. The structured output capability means you can ask for answers in a particular format. For example, you might prompt: “Give the answer as JSON: { "result": ..., "steps": [...]}” and Qwen2-Math will attempt to comply, organizing its solution into a JSON structure. Similarly, it can be instructed to output only a final answer or to separate the answer and explanation clearly. This makes it easier to integrate with other systems (like checking the final answer automatically, or displaying the stepwise solution in a UI). Keep in mind, structured output via natural language prompting isn’t 100% reliable, but Qwen2-Math’s training on plenty of formatted data gives it a better chance to follow such directives.

Capability Spotlight – Competition Math: To illustrate the power of Qwen2-Math, the 72B-Instruct model has demonstrated the ability to solve certain competition-level math problems (albeit simpler ones by contest standards). In the Qwen team’s case study, the model was able to tackle International Math Olympiad shortlist problems by reasoning through concepts like modular arithmetic and parity.

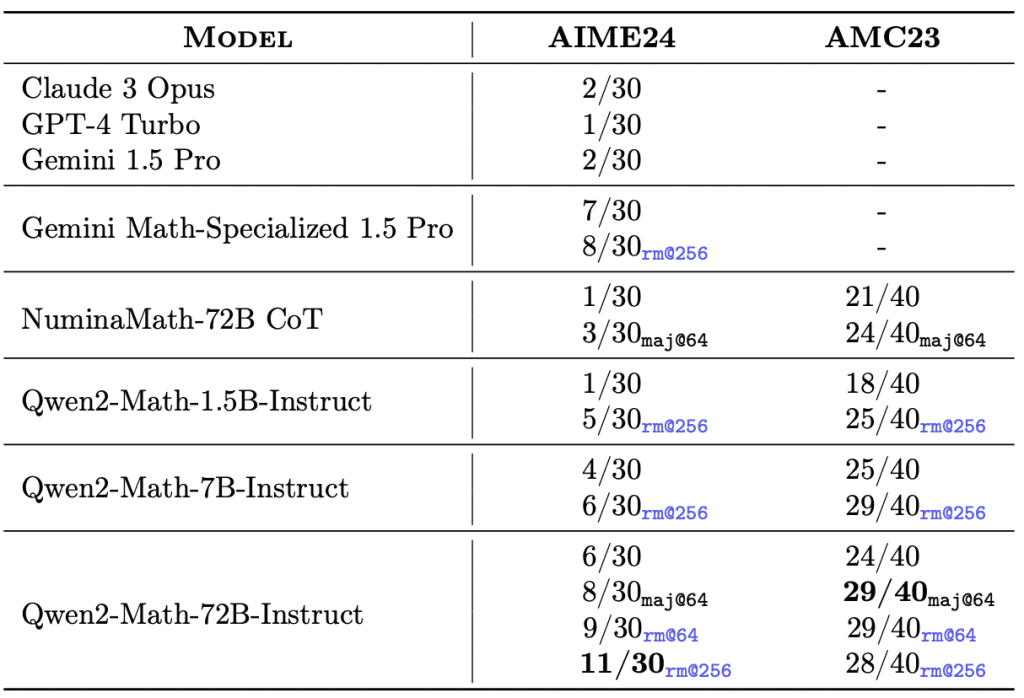
For example, one test problem asked for the smallest number of cube terms needed to sum to a huge power 200220022002^{2002}20022002. Qwen2-Math’s solution (generated without human correction) walked through prime factorization of 2002, considered cubes modulo 9, and reasoned out the answer step by step, complete with congruences and final conclusion. The model arrived at the correct answer ($4$ in that case) and presented the proof-like solution in a structured, logical way. While not every competition problem is within reach, this example shows that Qwen2-Math can handle non-trivial Olympiad-style reasoning, combining number theory insights with careful stepwise explanation.

This makes it a promising assistant for research or educational settings where explaining the solution is as important as getting the answer.

Example Inference Workflows

In this section, we’ll look at how to use Qwen2-Math in practice. We’ll demonstrate loading the model and querying it with Python (via the Hugging Face Transformers library), and also outline how one might integrate it through a REST API. These examples assume you have access to the model weights (downloaded from Hugging Face or ModelScope) and the necessary environment (a GPU for larger models).

Using the Hugging Face Transformers API

The easiest way to get started with Qwen2-Math is via Hugging Face’s Transformers library. The Qwen team has provided model files on Hugging Face Hub for the 1.5B, 7B, and 72B variants (both base and instruct). Below is a Python example showing how to load the 7B instruct model and run a simple query. This follows the official usage snippet from the model card:

from transformers import AutoTokenizer, AutoModelForCausalLM

model_name = "Qwen/Qwen2-Math-7B-Instruct"  # instruct variant for Q&A
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(
    model_name, torch_dtype="auto", device_map="auto"
)

# Example math prompt
prompt = "Find the value of $x$ that satisfies the equation $4x+5 = 6x+7$."

# For Qwen2-Math Instruct, we format the prompt as a chat conversation:
messages = [
    {"role": "system", "content": "You are a helpful assistant."},
    {"role": "user", "content": prompt}
]
# Apply Qwen's chat template formatting
formatted_input = tokenizer.apply_chat_template(messages, tokenize=False, add_generation_prompt=True)
inputs = tokenizer([formatted_input], return_tensors="pt").to("cuda")

# Generate a solution
outputs = model.generate(**inputs, max_new_tokens=256)
response = tokenizer.decode(outputs[0][inputs['input_ids'].size(1):], skip_special_tokens=True)
print(response)

Let’s break down what this does:

We load the tokenizer and model for "Qwen/Qwen2-Math-7B-Instruct". The device_map="auto" and torch_dtype="auto" will load the model across available GPU(s) in half-precision (which is typically required for 7B and larger due to memory constraints).

We define a prompt asking the model to solve a simple linear equation. Note the equation is written in LaTeX format within the string.

Because this is an instruction-tuned chat model, we package the prompt in the chat format Qwen2 expects. The library provides apply_chat_template to convert a list of role-based messages into the model’s internal prompt format. We include a system message (which can contain behavioral instructions; here we just set it as a generic helpful assistant) and the user message with our math question.

We then generate a response with model.generate(). We slice the outputs to get only the newly generated tokens (excluding the prompt tokens) and decode it to text.

Finally, we print the response. In this case, the output might be something like:

First, let's rearrange the equation: 
4x + 5 = 6x + 7 
Subtract 4x from both sides: 5 = 2x + 7 
Subtract 7 from both sides: 5 - 7 = 2x, so -2 = 2x 
Divide both sides by 2: x = -1 
$\boxed{-1}$

This demonstrates the model solving the equation step by step and giving the result. The exact format may vary, but the essential point is Qwen2-Math will show the work.

A few notes for this workflow:

• Ensure you have a new enough transformers library (v4.40+), as Qwen2 integration was added in recent versions.
• Loading the 7B model will require roughly 14–16 GB of GPU memory in half precision. The 1.5B model is much smaller (a few GB and could even run on CPU, albeit slowly), while the 72B model is extremely large (over 140 GB memory needed, typically run on a multi-GPU setup or with quantization techniques).
• The chat format with roles is needed for the Instruct models because they expect a conversation-like input (even if just one user query). If you use the base model (e.g., "Qwen/Qwen2-Math-7B" without “-Instruct”), you would just feed a raw text prompt and perhaps a few examples (few-shot) directly, since base models are not instruction-aligned.
• The output from the model often includes not just the final answer but also intermediate reasoning (as seen above). If you prefer just the answer, you can adjust the prompt to ask for brevity (e.g., “Solve … and give only the final answer.”). Conversely, if you want more detailed reasoning, you can prompt for that. The Instruct model usually finds a good balance by itself for math questions.

REST API Integration Example

In many real-world scenarios, you might deploy Qwen2-Math as a service and interact with it over an API. For instance, you could host the model on a server (or use Hugging Face Inference Endpoints) and send HTTP requests from your application to get solutions to math problems. While the exact setup can vary, here’s a conceptual example using a cURL request to a HuggingFace Inference API (assuming an instance of Qwen2-Math-7B-Instruct is deployed and you have an API token):

curl -X POST https://api-inference.huggingface.co/models/Qwen/Qwen2-Math-7B-Instruct \
  -H "Authorization: Bearer YOUR_HF_API_TOKEN" \
  -H "Content-Type: application/json" \
  -d '{
        "inputs": "Solve the equation $4x+5 = 6x+7$ for x, and explain your steps."
      }'

This HTTP POST sends a JSON payload with an "inputs" field containing our prompt (with LaTeX included). The service would then return a JSON response, typically containing a field like "generated_text" with the model’s answer. For example, the response might look like:

{
  "generated_text": "First, I'll rewrite the equation...\n...Therefore, $x = -1$."
}

You can then parse this in your application to extract the answer and display it.

If you deploy the model yourself (say, using a framework like FastAPI or Flask around the Transformers pipeline), your API might have an endpoint where you send a similar JSON or form-data request and get back the model output. The key is that Qwen2-Math accepts a plain string as input (with the special formatting for chat if needed) and returns a text string as output.

Notes on API usage:

• Make sure to include any necessary system instructions in the prompt if your deployment doesn’t automatically prepend them. For instance, the example above directly puts the problem in the input. If using the instruct model, it can often infer it’s a user query even if not in a chat format, but ideally, maintain the <system><user> structure if your API supports it.
• Watch out for input size limits. If using a hosted inference API, there might be limits on request size. Qwen2-Math can handle very long inputs (especially the big models), but the API endpoint might restrict payloads. If self-hosting, ensure your server can receive large requests if you plan to feed long contexts.
• Responses can be streamed in some setups (token by token generation). This is useful for real-time applications or a web UI where you want to show the solution as it’s being written out by the model.

By using either the direct Transformers interface or a REST API, developers can integrate Qwen2-Math into various environments – from Jupyter notebooks and backend services to web apps and mobile applications that call the model remotely.

Real-World Use Cases for Qwen2-Math

Qwen2-Math’s capabilities unlock a range of applications in software and research. Below are some developer-oriented use cases where this model can be particularly valuable:

Math Reasoning Engine in AI Agents: You can embed Qwen2-Math within an autonomous agent or chatbot that needs to solve math problems as part of its tasks. For example, a coding agent using an LLM might defer any math sub-problems to Qwen2-Math to ensure accurate calculation and reasoning. The chain-of-thought output can be parsed by the agent to decide next steps. This is useful in complex workflows (like a research assistant agent that plans experiments and needs to do calculations or derivations in the process).

Scientific Research Assistant: Researchers can use Qwen2-Math to assist in deriving formulas, checking computations, or explaining theoretical steps. For instance, in physics or engineering research, the model could help work through the algebra of a derivation, suggest how to simplify an expression, or verify whether two formulations are equivalent. Because Qwen2-Math can output LaTeX, it’s convenient to incorporate its results directly into research notes or publications. It essentially acts as a knowledgeable collaborator that can carry out tedious algebra and provide logical justifications in scientific problems.

Automated STEM Problem Solvers: Many educational technology applications require solving math and science problems automatically – for example, to generate solutions for an online homework platform or to build an interactive tutor. Qwen2-Math can serve as the core solver for such a system. Given a problem (from basic arithmetic up through advanced calculus or physics), it can produce the step-by-step solution that the platform can display to students. Its ability to reason like a human tutor (explaining each step) is a huge advantage here. It could also be used to create alternate solutions or hint sequences for problems, by prompting it appropriately.

Backend Service for Math APIs: One can create a cloud API where users submit math queries (like “Integrate sin^2(x) dx” or “Solve this optimization problem…”) and get results. Qwen2-Math would be the engine behind this API, interpreting the query and responding with the solution and explanation. Such an API could power a variety of front-end apps: a calculator app, a calculus problem solver website, a plugin in an education tool, etc. Because the model can handle a dialogue, the API could also support follow-up questions like “Explain step 3 in more detail” using the context of the conversation.

Developer Tools for Symbolic Computation: While traditional computer algebra systems (CAS) like Mathematica or Sympy are rule-based, an LLM like Qwen2-Math offers a different approach to symbolic math. Developers could integrate it to complement these systems – for example, use Qwen2-Math to tackle integrals or equations that are tricky for formal algorithms by having it suggest transformations or approaches. It might not always be as reliable as a CAS for absolute guarantees, but it can often creatively combine steps. A developer tool might use Qwen2-Math to provide quick reasoning or to explain the steps that a CAS took (translating a formal proof into natural language). Additionally, since Qwen2-Math can write code, it could even generate Sympy or Python code to perform a calculation (though Qwen2.5-Math’s tool integration is more direct on that front).

Automated Theorem Explanation & Proof Assistance: For math education software or even theorem-proving support, Qwen2-Math can be used to explain the steps of a proof or provide insights. For instance, given a theorem statement, you could ask Qwen2-Math to outline a proof strategy. Or if a student’s proof attempt is given, the model could try to fill in missing justifications. It’s not a formal proof assistant that guarantees correctness, but as a heuristic aid, it can make human-readable mathematical reasoning more accessible. Its chain-of-thought output is akin to a teacher writing out the reasoning on a whiteboard. This could also benefit those working in formal verification: the LLM can suggest the next logical step or a lemma in proving a certain property.

Each of these use cases highlights that Qwen2-Math is essentially a math reasoning specialist. Developers integrating it should leverage its step-by-step explanatory style and its comfort with formal notation. Whether it’s to power an educational app or to assist in scientific computing, Qwen2-Math provides a level of mathematical understanding that general LLMs often lack, especially at the smaller scales where open-source models are viable to run.

Prompt Patterns and Examples for Math Tasks

To get the best results from Qwen2-Math, it helps to phrase your prompts clearly and possibly include cues that trigger its chain-of-thought reasoning. Here are some prompt patterns and examples for different types of math tasks:

Algebraic Equation Solving: When asking the model to solve equations, you can simply state the equation and ask for the solution. For instance:
User Prompt: “Solve the equation 4x+5=6x+74x+5 = 6x+74x+5=6x+7 for xxx.”
Response: The model will likely rearrange the equation and solve, giving something like: “Subtract 4x4x4x from both sides to get 5=2x+75 = 2x + 75=2x+7. Then subtract 7: −2=2x-2 = 2x−2=2x. Divide by 2 to find x=−1x = -1x=−1.” It may conclude with x=−1x = -1x=−1.
You can add “Show your steps.” or “Explain each step.” to ensure it provides a derivation. By default, the instruct model often does show steps for non-trivial equations.

Calculus (Differentiation/Integration): The model can handle many calculus problems. For differentiation:
Prompt: “Differentiate y=3x2sin⁡xy = 3x^2 \sin xy=3x2sinx with respect to xxx.”
The model should apply the product rule and give: y′=6xsin⁡x+3x2cos⁡x.y’ = 6x\sin x + 3x^2 \cos x.y′=6xsinx+3x2cosx. It might write out the reasoning: “Using the product rule d(uv)/dx=u′v+uv′d(u v)/dx = u’v + uv’d(uv)/dx=u′v+uv′, here u=3x2u=3x^2u=3×2 and v=sin⁡xv=\sin xv=sinx, so…”. For integration:
Prompt: *“Evaluate the integral \int (2x^3 – x + 4)\,dx.\”* It should output something like: \( \frac{1}{2}x^4 – \frac{1}{2}x^2 + 4x + C. Again, it may show an intermediate step for each term’s antiderivative. If the integral is complex, it might explain a substitution or decomposition. Always check the result (especially the constant or any algebraic simplification) as minor mistakes can occur.

Symbolic Simplification: You can ask Qwen2-Math to simplify or factor expressions:
Prompt: “Simplify the expression x2−1x−1\frac{x^2 – 1}{x – 1}x−1×2−1​.”
Ideally, it will respond that x2−1x−1=x+1\frac{x^2-1}{x-1} = x+1x−1×2−1​=x+1 (with a note that x≠1x \neq 1x=1 due to the original denominator). It might explicitly factor x2−1x^2-1×2−1 as (x−1)(x+1)(x-1)(x+1)(x−1)(x+1) and then cancel the x−1x-1x−1 term. For factoring, e.g.:
Prompt: “Factor x3+2×2−x−2x^3 + 2x^2 – x – 2×3+2×2−x−2.”
It may try the rational root test or grouping and give the factorization (x2−1)(x+2)(x^2 – 1)(x + 2)(x2−1)(x+2) or further factor to (x−1)(x+1)(x+2)(x-1)(x+1)(x+2)(x−1)(x+1)(x+2). The chain-of-thought could show how it found roots x=1,−1,−2x=1,-1,-2x=1,−1,−2 by testing small integers.

Word Problem Reasoning: For narrative problems, it’s good to ensure the question is clearly asked at the end. For example:
Prompt: “Bob has 3 more apples than Alice. Together they have 21 apples. How many apples does each person have? Explain your reasoning.”
Qwen2-Math will likely assign variables (let AAA be Alice’s apples, BBB Bob’s), set up equations like B=A+3B = A + 3B=A+3 and A+B=21A + B = 21A+B=21, and solve to get A=9,B=12A = 9, B = 12A=9,B=12. It will explain each step and might even check the solution fits the conditions. Including “Explain your reasoning” guarantees it doesn’t just spit out the answer but shows the setup.

Logical/Proof-style Prompts: You can engage the model in more open-ended reasoning too. For instance:
Prompt: “Prove that the sum of two even numbers is always even.”
While this veers into proof writing, Qwen2-Math can handle simple proofs by example: it might say “Let the two even numbers be 2m2m2m and 2n2n2n. Their sum is 2m+2n=2(m+n)2m+2n = 2(m+n)2m+2n=2(m+n), which is divisible by 2, hence even.” This shows the model’s capacity for general logical reasoning in a mathematical context. For best results, a direct “Prove that…” works, but if it’s a known theorem it might just state the proof succinctly. You can also ask “Why is … true?” for more explanation style.

Step-by-Step with Hints: If you want the model to solve something but only reveal one step at a time (perhaps for tutoring purposes), you can prompt iteratively. For example:
First prompt: “How do we start solving x2−5x+6=0x^2 – 5x + 6 = 0x2−5x+6=0?”
It might respond with a hint like: “We look for factors of 6 that add up to 5. In this case, 2 and 3 work because 2+3=52+3=52+3=5. So we can factor the quadratic as (x−2)(x−3)=0(x-2)(x-3)=0(x−2)(x−3)=0.”
You can then continue: “Great. What are the solutions from (x−2)(x−3)=0(x-2)(x-3)=0(x−2)(x−3)=0?” and it will conclude x=2x=2x=2 or x=3x=3x=3. This interactive style is more of a dialogue and shows that Qwen2-Math can follow along a multi-turn solution if needed.

In all these patterns, clarity is key. Qwen2-Math is generally good at inferring what to do, but explicitly stating the task (“solve”, “simplify”, “calculate”, “explain”) helps. Also, because it was trained on both English and (soon) bilingual corpora, you can intermix some language if needed, but sticking to English for now is safest as the initial release mainly supports English. As Qwen2-Math 2.5 and beyond include Chinese, you could ask the question in Chinese and get a Chinese explanation as well, but we focus on English prompts here as per the model’s primary support.

Output Formatting and Structured Answers

Controlling the format of Qwen2-Math’s output can be important for integration into software or for meeting user expectations. Fortunately, the model is quite format-savvy due to its training. Here are some tips and features regarding output formatting:

LaTeX in Answers: As noted, Qwen2-Math will often use LaTeX markup for mathematical expressions in its answers by default. This is great if you want to display the answer on a web page or app with math rendering (like MathJax). For example, if the answer involves a fraction or exponent, expect it to appear as $\frac{...}{...}$ in the text. You typically don’t need to specifically ask for LaTeX; it will do it whenever it writes an equation or variable. If for some reason you want plain-text math (e.g. “sqrt(2)” instead of 2\sqrt{2}2​), you might have to explicitly instruct the model: “Give the answer without LaTeX, just plain text.” But in most cases, LaTeX is preferable for clarity.

Step-by-Step Explanations: By design, the instruct model usually provides step-by-step solutions. If you find the model giving just an answer without explanation and you need the steps, you can prompt it with phrases like “Show all steps”, “Explain your solution in detail”, or even prefix the user query with “Step-by-step:”. Conversely, if the model is too verbose and you only need a brief answer, instruct it not to show the work. For instance: “Solve x2=2x^2 = 2×2=2 and only give the final solution.” It should then ideally respond with just x=2x = \sqrt{2}x=2​ or x=±2x = \pm \sqrt{2}x=±2​ (depending on interpretation) without the derivation. The ability to toggle verbosity is useful for different contexts (detailed solutions vs. quick answers).

Structured Output (Lists, JSON, etc.): Qwen2-Math can format answers as bullet points or numbered lists if asked. For example, if a problem asks for multiple answers or an analysis, the model might respond with a list:

Step 1: …

Step 2: …

Answer: …
This is helpful for breaking down solutions in a UI. Additionally, you can ask the model to output JSON or XML if you need machine-readable answers. While the model doesn’t have a guaranteed JSON mode, it often succeeds for simple structures. For instance:
Prompt: “Calculate the discriminant of ax2+bx+c=0ax^2+bx+c=0ax2+bx+c=0 and output as JSON: { "discriminant": value }.”
The model might respond with: { "discriminant": "b^2 - 4ac" } – it might put quotes around the expression or not, but generally it tries to follow the format. You would need to verify the JSON is valid, as the model might include extra commentary if not prompted strictly.

Final Answer Boxing: In many solutions, especially longer ones, Qwen2-Math will put the final answer in a boxed format or clearly separate it. For example, after a long derivation it might conclude with: $$\boxed{4}$$ to indicate the answer is 4. This convention comes from math write-ups and is useful to quickly locate the final result. When parsing answers programmatically, you can look for such markers (like \boxed{} or even phrases like “Thus, the answer is 4.”).

Handling Errors and Revisions: The model can sometimes correct itself in the output. For example, it might say “(Oops, I made an arithmetic mistake, let me fix that…)”. This is part of the conversational aspect. If you prefer it not do this (maybe you want only the polished solution), in your system role or prompt instructions you can say “If you make a mistake in the computation, correct it seamlessly without apologizing.” Usually though, the model’s final answer will be correct if it catches an error mid-way. The self-correction can be insightful to watch as it shows the model’s internal reasoning process.

In practice, to achieve a certain format, prompt engineering is key. Clearly state the desired format in the prompt. For instance: “List the solution steps as bullet points, then give the final answer on a separate line.” Qwen2-Math is quite likely to follow such instructions, outputting a nice bullet list and then something like “Answer: 42”. The ability to yield structured, well-formatted responses is one reason Qwen2-Math is developer-friendly – it reduces post-processing work to structure the output.

Limitations and Best Practices

While Qwen2-Math is a powerful tool, developers should be aware of its limitations and follow best practices to get the most out of it:

Limitations:

Not Guaranteed 100% Correct: Despite the rigorous training and high benchmark scores, Qwen2-Math can still make mistakes. These could be arithmetic slips (especially in long calculations), algebraic errors, or logical leaps. For instance, on very complex problems or edge cases, the model might propose a flawed solution or get the wrong answer. Always verify critical results, especially if the outcome will be used in an important setting. The model’s outputs have high accuracy on many test sets, but they are not infallible.

Lacks External Tool Precision: Qwen2-Math (v2.0 series) relies purely on its internal reasoning for calculations. This means for tasks like finding roots of high-degree polynomials, computing large numerical values, or tasks like finding eigenvalues of a matrix, it might be unreliable. The enhanced Qwen2.5-Math series introduced tool integration (like running Python code for exact computation), but in Qwen2-Math, there is no calculator under the hood – it’s all learned approximation. So, treat it as you would a human student: great at reasoning and providing insight, but prone to calculation errors on very demanding tasks.

Specialized Domain (Math/Logic) Only: As mentioned, Qwen2-Math is not a general chatbot. Its knowledge and skills are skewed towards math and STEM problems. If you ask it about a topic outside math, it may underperform or produce less reliable output than a general model. The Qwen team explicitly states the math models are meant for math problem solving and not recommended for other tasks. So if your application also needs open-ended conversation or knowledge in humanities, you might need to run a general model in parallel or switch models accordingly.

Resource Intensive (for Large Models): The 72B variant is extremely powerful in math reasoning, but using it requires significant hardware (multiple high-end GPUs or TPU pods). Even the 7B model, while much smaller, needs a decent GPU for fast responses. On CPU, inference would be very slow. There are quantized versions (e.g., 4-bit or 8-bit) that can reduce memory at some accuracy cost, which the community has produced. Be mindful of this when deploying – maybe use the 7B for real-time inference, and use 72B offline for research or batch jobs where the highest accuracy is needed.

English-Centric (for now): The initial Qwen2-Math release mainly supports English-language math problems. If you ask questions in other languages, the results might be mixed. Chinese support was announced to be coming soon (and indeed Qwen2.5-Math supports Chinese fully), but if you need bilingual support in the Qwen2-Math series, check for the latest model releases. Always ensure the model you choose matches your language needs (the model card or documentation will specify if bilingual).

Best Practices:

Use the Instruct Model for QA: Unless you have a specific reason to use the base model, prefer the Qwen2-Math-Instruct variants for querying. They are much better at following instructions like “show steps” and handling user-friendly interactions. The base model might require careful prompt engineering or few-shot examples to produce the same quality of reasoning.

Few-Shot Prompting for Tough Problems: If you have a very complex problem, providing a few examples of solved problems (chain-of-thought demonstrations) in the prompt can boost performance. For example, if you need it to solve an Olympiad geometry problem, you might precede the question with a smaller geometry problem and its solution steps as an illustration. This was actually the technique used in their benchmark evaluations. It helps the model know what format and approach to take.

Guide the Format in the Prompt: As discussed in the output formatting section, explicitly instructing the model on how to answer can save time. If you integrate Qwen2-Math into an app, you can have a hidden preamble that sets the style. For instance: “You are a math solver bot. Always provide a step-by-step solution, and then give the final answer in a box at the end.” This way, every answer is consistent without the user needing to specify it each time.

Verify and Cross-Validate: For mission-critical applications, consider adding a verification step. This could be as simple as plugging the model’s numeric answer back into the original equation to see if it satisfies it (the model sometimes does this itself in its solution). Or you can run a secondary method: e.g., if Qwen2-Math gives a result for an integral, you could differentiate it using a CAS to confirm it matches the integrand. Another approach is majority voting or sampling – generate multiple answers with slight prompt variations or different random seeds (for nondeterministic sampling) and see if they agree. The Qwen2 training reports indicate that picking the highest reward solution out of several (RM@N) gave better results than even majority voting, but that requires having the reward model. For most developers, a simpler ensemble of a few runs and checking consistency can increase confidence in the output.

Stay Updated with Latest Versions: The Qwen family is evolving rapidly. Qwen2.5-Math introduced new features like tool use and improved accuracy. Always check if a newer model is available and evaluate if it fits your needs better. However, also mind the compatibility (the 2.5 models might require the newer Qwen2.5 base, which they do, and possibly newer transformers support). If you upgrade, read the technical report or changelog – for example, Qwen2.5-Math can call Python for calculations, which may require an execution environment. For a stable deployment that doesn’t require that, Qwen2-Math might be simpler to manage.

Ethical and Correctness Considerations: Even though math seems apolitical, be aware that the model can still generate incorrect or misleading content. If used in an educational context, it should ideally be supervised or reviewed by an expert. One wouldn’t want to inadvertently teach a student the wrong method. Also, if integrating into homework solvers, consider the educational impact (perhaps provide just hints or steps and not just final answers to encourage learning).

By understanding these limitations and guidelines, you can harness Qwen2-Math’s strengths while mitigating potential downsides. In essence, treat it as a very knowledgeable but sometimes quirky math assistant: double-check its work, give it clear instructions, and it will greatly amplify your ability to handle complex mathematical reasoning in software.

Developer FAQs

Finally, let’s address some frequently asked questions that developers might have about Qwen2-Math:

This concludes our deep dive into Qwen2-Math. We’ve explored what makes it tick under the hood, how to use it effectively, and how it can be applied in real-world developer scenarios.

Qwen2-Math represents a significant step towards LLMs that can serve as reliable mathematical reasoners, and it provides a valuable tool for anyone looking to build applications that require understanding and solving math problems.

With careful integration and some best practices, Qwen2-Math can greatly enhance the mathematical capabilities of your AI projects.