Qwen2.5-Math

Qwen2.5-Math is an open-source series of large language models specialized in advanced mathematics and symbolic reasoning. Developed as part of Alibaba’s Qwen family in late 2024, Qwen2.5-Math comes in multiple model sizes (1.5B, 7B, and 72B parameters) and includes both base models and instruction-tuned variants.

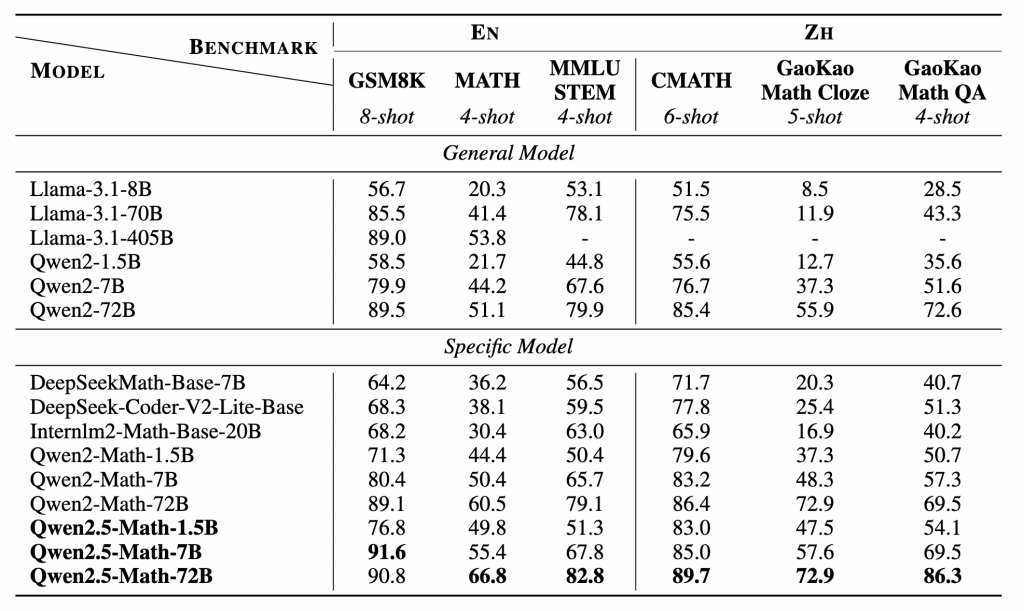
Unlike its predecessor (Qwen2-Math, which was limited to chain-of-thought reasoning in English), Qwen2.5-Math supports both Chain-of-Thought (CoT) and Tool-Integrated Reasoning (TIR) strategies to solve math problems in both English and Chinese. This expanded reasoning toolkit, along with a massive increase in training data (over 1 trillion tokens of math-focused text, up from 700B in Qwen2-Math), leads to substantially improved accuracy on challenging math benchmarks.

Qwen2.5-Math now ranks among the strongest math-specific LLMs publicly available, often outperforming prior open models and even matching the capabilities of some proprietary systems on competition-level problems.

Importantly, Qwen2.5-Math is purpose-built for mathematical reasoning – the authors do not recommend using it for general tasks beyond math. This introduction provides a high-level overview of Qwen2.5-Math’s architecture and features, followed by detailed sections on its symbolic math skills, equation solving abilities, word problem reasoning, output formatting options, and integration examples.

The goal is to equip developers and researchers with a comprehensive technical guide to Qwen2.5-Math’s capabilities and how to leverage them in scientific and engineering applications.

High-Level Math-Focused Architecture

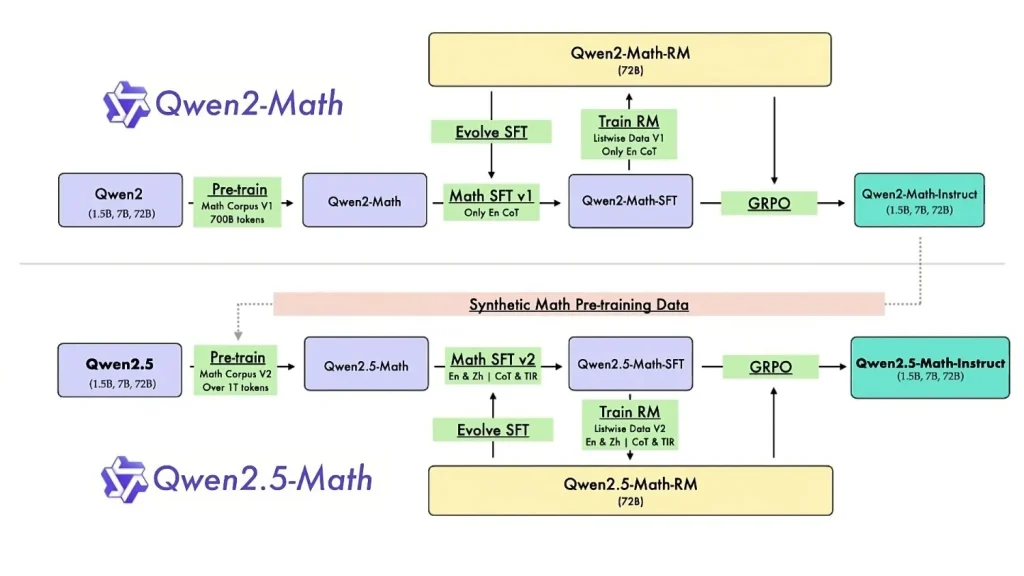
At its core, Qwen2.5-Math adopts the same transformer-based decoder architecture as the base Qwen2.5 LLM, but with targeted specialization for mathematical tasks. The model uses a dense, decoder-only Transformer with a context window of 4K tokens for math reasoning, and it has been trained on a Math Corpus v2 exceeding 1 trillion tokens of high-quality mathematical text (from textbooks, web data, code, etc.).

This represents a significant expansion over the previous generation’s 700B-token math corpus. The training pipeline (see Figure above) first produces base math models (1.5B, 7B, 72B) through additional pre-training of Qwen2.5 on the curated math corpus. Then, an instruction-tuning phase produces Qwen2.5-Math-Instruct models by supervised fine-tuning (SFT) on problem-solution data and applying reinforcement learning with human feedback. In particular, a Qwen2.5-Math-RM-72B reward model was trained to judge the quality of mathematical reasoning, and used in a rejection sampling and Group Relative Policy Optimization (GRPO) loop to refine the instruct model’s outputs. This alignment process optimized the model to produce helpful step-by-step solutions and accurate answers in response to natural language math queries.

The resulting architecture is math-focused in both its training data and its reasoning mechanisms. Qwen2.5-Math not only learned standard language modeling patterns, but also was explicitly taught to employ advanced reasoning methods: it can carry out chain-of-thought (CoT) reasoning (i.e. unpacking a solution in intermediate steps) and even invoke external tools or calculations via program-of-thought (PoT) or tool-integrated reasoning. In practice, the Tool-Integrated Reasoning (TIR) capability means the model can incorporate computational tools or delegate certain calculations to external programs when needed for complex problems.

(For example, finding the exact roots of a polynomial or the eigenvalues of a matrix might be handled by having the model generate a piece of code or a formula to be evaluated externally.) The architecture supports this by allowing special prompting (discussed later) that cues the model to intermingle natural language reasoning with programmatic steps. Overall, the high-level design of Qwen2.5-Math is geared toward being a “mathematical expert” model, combining a powerful language backbone with specialized data, reasoning strategies, and an alignment process tailored to mathematical problem solving.

Symbolic Reasoning Capabilities

One of Qwen2.5-Math’s core strengths is symbolic math reasoning – the ability to manipulate algebraic expressions, formulas, and mathematical symbols through logic rather than brute-force numeric computation. Thanks to the incorporation of chain-of-thought training and tool usage, Qwen2.5-Math can handle tasks like simplifying expressions, factoring polynomials, solving equations symbolically, and carrying out algebraic derivations.

For instance, the model can transform an expression like x2−5x+6x^2 – 5x + 6×2−5x+6 into its factored form, or solve for xxx in a quadratic equation analytically. It has demonstrated proficiency in precisely these kinds of tasks that often stump vanilla LLMs; by internally reasoning about the structure of the problem, it avoids the common pitfalls of purely language-based guessing. The developers note that while chain-of-thought (CoT) greatly improves reasoning, it alone may still struggle with rigorous symbolic calculation (e.g. exactly solving a higher-degree polynomial or computing an eigenvalue). To address this, Qwen2.5-Math’s enhanced tool-integrated reasoning allows it to invoke external computation when necessary, yielding far greater accuracy on symbolic problems. In practice, this might mean the model’s solution includes a snippet of Python to do long division of polynomials or a call to a library for solving an equation – effectively blending symbolic AI with programmatic power. The result is improved reliability in symbolic manipulations and complex algorithmic math: Qwen2.5-Math can carry out multi-step proofs or derivations, reason about limits and series, and generate answers that are not only logically sound but also exact.

Many of these capabilities were benchmarked in the MATH dataset and other exams, where the model achieved high scores (e.g. up to 87.8% on MATH at 72B with tool usage enabled), reflecting its expert-level mastery of symbolic reasoning tasks. For developers, this means Qwen2.5-Math can serve as a powerful engine for tasks like verifying algebraic identities, simplifying complex expressions, or assisting in formal math problem solving where step-by-step symbolic logic is required.

Equation Solving (Algebra to Calculus)

A prominent application of Qwen2.5-Math is solving mathematical equations – from basic algebra up through calculus and beyond. The model is adept at algebraic equation solving, handling linear and quadratic equations, systems of equations, and even exponential/diophantine equations, as illustrated in the figure above.

When presented with an equation or system, Qwen2.5-Math will typically show its work: it can isolate variables, simplify terms, and logically derive the solution step by step. For example, given a linear equation like 4x+5=6x+74x + 5 = 6x + 74x+5=6x+7, the model can reason through subtracting 4x4x4x from both sides, collecting terms, and solving for the variable (yielding x=−1x = -1x=−1), usually explaining each step in natural language. This stepwise algebraic reasoning extends to more advanced problems as well – the model can solve quadratic equations by identifying factoring opportunities or applying the quadratic formula, and it can tackle systems of linear equations using substitution or elimination methods. The chain-of-thought fine-tuning ensures that Qwen2.5-Math doesn’t just spit out the answer, but actually walks through the algebra, which is invaluable for transparency in scientific contexts.

Beyond algebra, Qwen2.5-Math exhibits strong capabilities in calculus and analysis problem solving. It can perform differentiation and integration tasks, often providing the result in closed-form. For instance, if asked to differentiate a function f(x)=exsin⁡xf(x) = e^x \sin xf(x)=exsinx, the model can apply the product rule and output the derivative f′(x)=exsin⁡x+excos⁡xf'(x) = e^x \sin x + e^x \cos xf′(x)=exsinx+excosx, potentially formatting the result in LaTeX for clarity.

Similarly, it can attempt indefinite integrals of reasonable complexity, explaining substitution or integration by parts if prompted to show reasoning. On definite integrals or more complex calculus problems (like series convergence or differential equations), the model uses its training on advanced math texts to guide the solution. While it may not always find a closed-form solution (especially if one doesn’t exist in elementary terms), Qwen2.5-Math often will outline the method – for example, setting up an integral for evaluation or using a series expansion argument. Thanks to the tool integration aspect, it may even offload heavy lifting (like numerically evaluating an integral or solving a differential equation) to an external solver if integrated appropriately.

In benchmarks like GSM8K (grade-school math word problems) and MATH (competition-level problems covering algebra, calculus, etc.), Qwen2.5-Math significantly outperformed its predecessors, demonstrating a high success rate in both straightforward equation solving and multi-step calculus reasoning. For developers, this means the model is suitable as a backend “math engine” for solving equations programmatically – whether one needs to compute the roots of an equation within a larger application or to automatically solve calculus problems in an educational tool. The key advantage is that Qwen2.5-Math can provide the derivation of the answer, not just the final number, which is crucial for verification and learning.

Word Problem Reasoning

Another area where Qwen2.5-Math excels is in interpreting and solving math word problems stated in natural language. These problems require the model to parse a textual scenario or question, formulate the mathematical problem hidden within, and then solve it. Qwen2.5-Math’s training on chain-of-thought solutions has particularly enhanced its performance on such tasks by enabling it to break down complex word problems into logical steps. When given a problem like:

“A tank can be filled by one pipe in 3 hours and by another pipe in 6 hours. How long will it take to fill the tank if both pipes are opened together?”

Qwen2.5-Math can identify the relevant rates (tank/hour), set up the equation 1/3+1/6=1/t1/3 + 1/6 = 1/t1/3+1/6=1/t, and solve for the combined time t=2t = 2t=2 hours, typically narrating the reasoning: e.g. “Pipe A fills 1/3 of the tank per hour, Pipe B fills 1/6 per hour, together that’s 1/3+1/6=1/2 per hour, so the tank is full in 2 hours.” This ability to interpret narrative and translate it into equations is powered by the model’s large training on word-problem datasets (like GSM8K) and its bilingual competence (it can do the same with Chinese-language word problems from exams like Gaokao Math). The model uses natural language understanding to pick out quantities, relationships, and the question being asked, then uses its math reasoning to solve stepwise.

Crucially, Qwen2.5-Math doesn’t require a user-provided solution template; it can figure out the approach (algebra, arithmetic, proportional reasoning, etc.) on its own. For multi-step problems (e.g. a geometry problem that needs an intermediate result to plug into another formula), the chain-of-thought prompting helps it not skip steps. It will explicitly solve sub-problems in sequence. For example, in a geometry word problem it might first derive a necessary length via the Pythagorean theorem, then use that result to compute an area, explaining each sub-calculation.

The instruct model is tuned to present these solutions in a coherent, step-by-step manner, as if it were a tutor showing the work. This is extremely useful for researchers or educators who want not just an answer but an explanation. In terms of performance, Qwen2.5-Math’s word problem solving is among the best in class for open models – its scores on benchmarks like GSM8K (grade school math) indicate a high accuracy with chain-of-thought, and it has even tackled Olympiad-level problems in evaluations. That said, extremely complex linguistic puzzles or problems requiring real-world knowledge outside pure math could still pose challenges (since the model is math-focused, it might not handle tricky riddles that hinge on common-sense rather than mathematical logic).

For typical mathematical word problems though, developers can rely on Qwen2.5-Math to parse and solve them, and even integrate the model in an application that automatically turns user-written questions into solved steps and answers. Prompt engineering (next section) can further refine how the model explains its reasoning in such scenarios.

LaTeX and Structured Output Features

A notable feature of Qwen2.5-Math is its ability to output well-formatted mathematical content, including LaTeX-formatted equations and even JSON-structured answers if requested. Given the technical audience for its outputs, the model was trained and aligned to produce clean mathematical notation. For example, if asked a question about integrals or matrices, Qwen2.5-Math will often present the result using LaTeX syntax for readability (e.g. “∫01x2dx=13\int_0^1 x^2 dx = \frac{1}{3}∫01​x2dx=31​”). It even follows formatting instructions such as putting the final answer inside a \boxed{} if the prompt suggests it, which is a common convention in math write-ups.

The model’s familiarity with LaTeX is a byproduct of its training on scientific texts and the fine-tuning process that encouraged it to provide answers in a professional format. This is extremely useful for applications like scientific report generation or publishing workflows, where the output from the model can be directly embedded into documents. Developers can explicitly prompt the model with instructions like “Give the final answer in LaTeX format” to ensure the answer is rendered as a LaTeX math expression. In our experience, Qwen2.5-Math will typically comply, wrapping its equations in \( ... \) or $$ ... $$ as appropriate, or using special symbols correctly.

Beyond LaTeX, Qwen2.5-Math can also produce structured outputs such as JSON, which is valuable for programmatic use of its results. For instance, if you want the model to return an answer along with a step-by-step solution in a machine-readable format, you could prompt: “Solve the problem and return the result as a JSON object with fields steps and answer.” The model might then output something like:

{
  "steps": [
    "Let’s denote the unknown number as x.",
    "From the problem, we have the equation 2x + 5 = 17.",
    "Solving for x, we get 2x = 12, so x = 6."
  ],
  "answer": 6
}

This structured-response capability is enhanced by certain API features as well. When using Alibaba’s ModelStudio API (DashScope) or an OpenAI-compatible endpoint, you can actually enforce a JSON response format by setting a parameter and including the word “JSON” in the system prompt. Qwen2.5-Math (especially the base Qwen2.5 models) supports a special JSON mode where it guarantees the output is valid JSON without extra text. This is incredibly helpful in building automation pipelines – for example, a backend service can get a JSON answer from the model and directly use the numeric results or the solution steps in another application (such as grading, verification or visualization). However, note that the math-instruct models use “thinking” mode (chain-of-thought), which in some cases might need careful prompting to keep the output strictly JSON.

In practice, simply asking the model for JSON and using the API’s format enforcement yields good results, as long as the prompt explicitly says e.g. “output only a JSON object with the answer”. In summary, Qwen2.5-Math is flexible in its outputs: whether you need elegant LaTeX for a human reader or structured data for a machine pipeline, the model can accommodate those needs with the right prompting or API settings. This makes it straightforward to integrate into scientific computing workflows where downstream components might consume the model’s output.

Python Integration Examples

One of the strengths of Qwen2.5-Math is that it can be readily integrated into Python-based workflows, either via the Hugging Face transformers library or through API SDKs. Below we provide a few code examples to demonstrate how developers can load the model and use it for math problem solving with step-by-step reasoning and nicely formatted outputs.

First, let’s see how to load a Qwen2.5-Math instruct model locally using Hugging Face Transformers. We’ll use the 7B instruct model for illustration (since 72B is resource-intensive), assuming you have the model weights available:

from transformers import AutoModelForCausalLM, AutoTokenizer

model_name = "Qwen/Qwen2.5-Math-7B-Instruct"
device = "cuda"  # or "cpu", depending on your hardware

# Load the model and tokenizer
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(
    model_name, torch_dtype="auto", device_map="auto"
)

# Prepare a math problem prompt
problem = "Find the value of $x$ that satisfies the equation $4x + 5 = 6x + 7$."

# Use a system message to request step-by-step reasoning and LaTeX formatting
messages = [
    {"role": "system", "content": "You are a math assistant. Solve the problem step by step and put the final answer in LaTeX \\boxed{} format."},
    {"role": "user", "content": problem}
]

# Convert messages to the model's chat format and generate a response
formatted_input = tokenizer.apply_chat_template(messages, tokenize=False, add_generation_prompt=True)
inputs = tokenizer([formatted_input], return_tensors="pt").to(device)
outputs = model.generate(**inputs, max_new_tokens=256)
response_text = tokenizer.batch_decode(outputs, skip_special_tokens=True)[0]
print(response_text)

In this snippet, we construct a conversation with a system role prompt instructing the model to reason stepwise and output the final answer in a LaTeX \boxed{}. The tokenizer.apply_chat_template function helps format the chat input properly for Qwen’s dialogue style. After generation, response_text will contain the model’s full solution. For the example equation 4x+5=6x+74x+5=6x+74x+5=6x+7, the output might look like:

First, let’s bring like terms together. Subtract \(4x\) from both sides: \(5 = 2x + 7\). 
Now subtract 7 from both sides: \(5 - 7 = 2x\), so \(-2 = 2x\). 
Divide both sides by 2: \(x = -1\). 

Therefore, the solution is \(\boxed{-1}\).

As shown, the model provided a clear chain-of-thought solution and formatted the final answer neatly in \(\boxed{-1}\). This approach can be used for more complex problems as well – simply adjust the prompt. For instance, if solving an integral, you might set problem = "Integrate $\\int x e^x dx$" and the system content to “show each step and provide the final antiderivative in LaTeX”. The model will then output the integration process and result (e.g. xex−ex+Cx e^x – e^x + Cxex−ex+C in a LaTeX format).

It’s worth noting that resource requirements for running these models are non-trivial: the 7B model typically fits on a single high-end GPU (around 15 GB VRAM needed in FP16), whereas the 72B model requires multiple GPUs or distributed setup (on the order of 160–192 GB total VRAM for FP16). Developers can consider using techniques like 4-bit quantization or offloading layers to CPU to run the larger models if needed, or simply use the 7B for development and call a hosted API for the 72B model when full power is required. The Hugging Face integration shown above works for all model sizes (transformers >= 4.37 has built-in Qwen support), so the main difference is just hardware capability.

REST API Integration Examples

Qwen2.5-Math can also be accessed via RESTful APIs, which is convenient for deploying it as part of a web service or scientific computing pipeline. Alibaba Cloud provides an OpenAI-compatible API (through Model Studio/DashScope) where Qwen models can be invoked by name. In addition, one can host the model and expose an endpoint manually. Below are examples demonstrating typical API usage patterns: solving a problem via a chat completion call, and requesting a structured output (JSON) from the model.

Example 1: Basic Chat Completion (Math Reasoning) – using an OpenAI-compatible Python SDK:

import openai
openai.api_key = "YOUR_API_KEY"
openai.api_base = "https://dashscope-intl.aliyuncs.com/compatible-mode/v1"  # endpoint for Alibaba Cloud int'l

# Compose the conversation payload
messages = [
  {"role": "system", "content": "You are a helpful mathematical assistant."},
  {"role": "user", "content": "Solve the equation 2x^2 - 5x - 3 = 0 and explain your steps."}
]

response = openai.ChatCompletion.create(
    model="qwen2.5-math-7b-instruct",
    messages=messages,
    temperature=0.0  # deterministic output for reasoning
)
answer = response['choices'][0]['message']['content']
print(answer)

In this example, we call the ChatCompletion.create with the Qwen2.5-Math instruct model. The system prompt sets the role, and the user prompt asks the model to solve a quadratic equation with explanation. The model’s response (in answer) would be a step-by-step derivation, likely something along the lines of: “To solve 2×2−5x−3=02x^2 – 5x – 3=02×2−5x−3=0, we can factor it as (2x+1)(x−3)=0(2x+1)(x-3)=0(2x+1)(x−3)=0. This gives solutions x=−12x = -\frac{1}{2}x=−21​ or x=3x = 3x=3.” (The actual wording may differ, but it will include an explanation.) Using temperature 0 ensures the solution is consistent and not random, which is often desirable for math problems.

Example 2: Requesting JSON Structured Output via REST – sometimes we want the model’s answer in a machine-parsable format. The following shows how one might enforce a JSON answer:

messages = [
  {"role": "system", "content": "You are a math solver. Provide the answer in JSON format."},
  {"role": "user", "content": "What is the prime factorization of 360? Return the result as JSON."}
]
response = openai.ChatCompletion.create(
    model="qwen2.5-math-7b-instruct",
    messages=messages,
    response_format={"type": "json_object"}  # ask API to enforce JSON response
)
json_answer = response['choices'][0]['message']['content']
print(json_answer)

Here we set the system instruction to explicitly mention JSON, and we use the response_format={"type": "json_object"} parameter which the Model Studio API supports for certain models. If Qwen2.5-Math supports this mode, the result stored in json_answer will be a JSON string, for example:

{ "number": 360, "prime_factors": [2, 2, 2, 3, 3, 5] }

This indicates 360=23×32×5360 = 2^3 \times 3^2 \times 5360=23×32×5. The ability to get structured JSON directly is extremely useful – it means downstream code can easily parse the factors array, etc., without having to regex the model’s text output. (If the API refused the request because the model is in thinking mode, one workaround is to instruct the model in the prompt to only output a JSON and parse the text manually – but the response_format helps avoid any extra text like markdown or explanation).

The above REST examples use Python for clarity, but of course you could use curl or any HTTP client to send a similar JSON payload to the endpoint. The OpenAI chat completion format is supported, so integration is straightforward if you’ve used OpenAI’s API before. Just be sure to specify the correct model name (e.g., "qwen2.5-math-72b-instruct") and include your API credentials. In summary, whether via direct library calls or through a web service, Qwen2.5-Math can be deployed in various environments, enabling flexible math inference workflows – from a backend microservice that solves equations on demand, to an interactive scientific assistant in a notebook environment.

Prompt Engineering for Math Tasks

Effective prompt engineering is key to getting the most out of Qwen2.5-Math, especially given its advanced reasoning capabilities. Here are some tips and patterns for crafting prompts and system messages that guide the model to produce optimal results:

Encourage Step-by-Step Reasoning: To leverage chain-of-thought, explicitly instruct the model to reason step by step. This can be done via the system role (e.g. “Please reason step by step”) or by appending something like “Let’s think this through step by step.” in the user prompt. Qwen2.5-Math is tuned to follow such cues and will output a detailed solution process rather than just an answer. For complex problems, this greatly improves accuracy, as the model will lay out intermediate steps and reduce errors.

Activate Tool Integration when Needed: If you suspect a problem may require calculation beyond the model’s mental math (for example, a complicated arithmetic or a need for brute-force search), you can invoke the tool-integrated reasoning mode. This is done by a system message like “Use natural language reasoning and necessary calculations (you may execute programs) to solve this.”. Internally, this prompt signals the model that it can output a snippet of code or a calculation result directly. In a controlled setting (like using the model through an API with a tool plugin), the code could be extracted and executed. If you’re not actually executing code, the model might still simulate the calculation. Use this mode sparingly for cases where pure reasoning might falter on accuracy.

Specify Output Format: As discussed, Qwen2.5-Math is very flexible with output format if you tell it exactly what you want. Always mention in the prompt if you need LaTeX: e.g., “give the answer in LaTeX format” or “surround the final answer with \( \)”. Similarly, for JSON or structured outputs, indicate that clearly (and ensure the word “JSON” appears if using the enforcement parameter). The model will generally obey format instructions. You can also ask for things like: “Answer only with a numeric value.” if you want to suppress the reasoning and just get a number (the instruct model might still produce some explanation, but you can reduce that with such instructions and by using temperature=0).

Few-Shot Examples: Although Qwen2.5-Math is quite capable zero-shot, providing a few examples in the prompt can help in certain scenarios. For instance, if you want a specific style of solution or you want to bias the model toward a certain reasoning approach, you can include a QA pair or two as demonstration. Because the context window is large (4k tokens, potentially more), you have room for including sample problems with solutions. Make sure to separate them clearly and then present the new problem. The model will analogize from the given examples. This can improve performance on niche problem types or formats that might not be in the training distribution.

Clarity in Problem Statement: Since the audience is likely to be feeding the model programmatically, ensure the problem statement given to the model is clear and unambiguous. For word problems, sometimes rephrasing the question in a simpler way (or adding a line like “Here is the problem in simpler terms: …”) can help the model parse it correctly. Qwen2.5-Math is quite good linguistically (being based on a general LLM), but if a question is convoluted or contains irrelevant details, consider cleaning it up with a pre-processing step or an initial prompt that tells the model to focus on the math relevant info.

Managing Hallucinations: While rare on math-focused prompts, LLMs can sometimes hallucinate steps or facts. If you notice the model tends to stray (e.g., introducing a fact that isn’t in the problem), tighten the prompt. You can say: “If any information is missing, state that it’s not solvable rather than making assumptions.” This kind of instruction can prevent the model from making unwarranted leaps. Also, using deterministic decoding (temperature 0) for math is generally recommended to avoid random mistakes.

By applying these prompt engineering strategies, developers and researchers can significantly enhance Qwen2.5-Math’s reliability and tailor its responses to their specific use case. The model responds well to clear, specific instructions – treat it like a very knowledgeable but obedient assistant: it will follow your lead on format and approach. So, whether you need a verbose proof or a succinct answer, the right prompt will yield it.

Performance Considerations (Accuracy, Stability, Edge Cases)

From a performance standpoint, Qwen2.5-Math has proven to be a top-tier performer on a variety of mathematical reasoning benchmarks. The 72B-instruct model (the largest variant) currently leads most open-source models on math tasks – for example, it achieves about 92.9 on the MATH competition benchmark under tool-assisted evaluation, essentially reaching an expert level. Even the smaller models are impressive: the 7B-instruct model scores in the mid-80s on MATH (e.g. 85.3 with tool integration), and around high 70s to low 80s on GSM8K, indicating strong performance on both competition math and grade-school problems. These numbers mean Qwen2.5-Math can solve the majority of problems in those sets correctly.

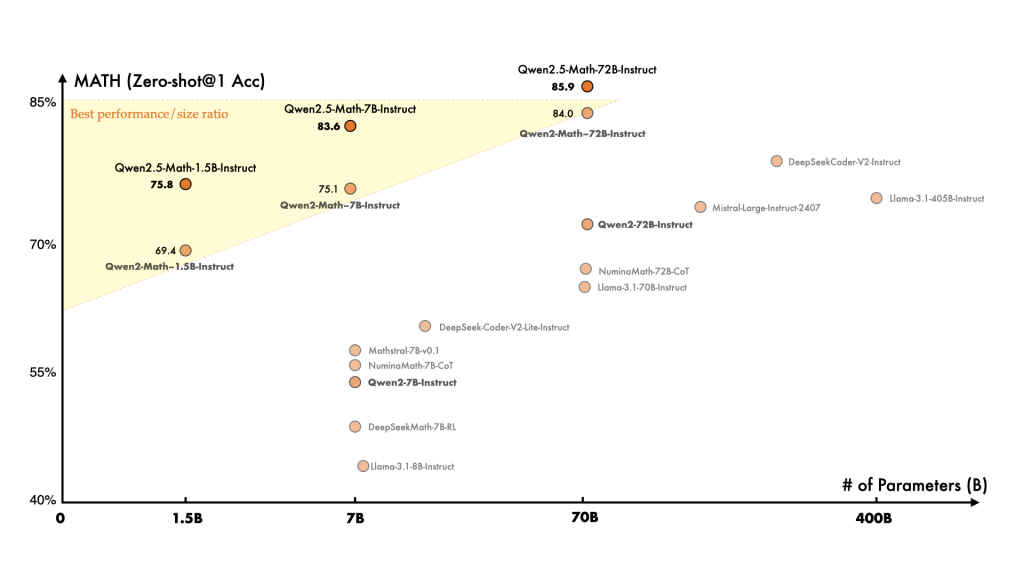
Moreover, internal evaluations showed it outperforming the previous generation (Qwen2-Math) by significant margins – e.g. a +5 to +12 point boost on various benchmarks after the upgrade.

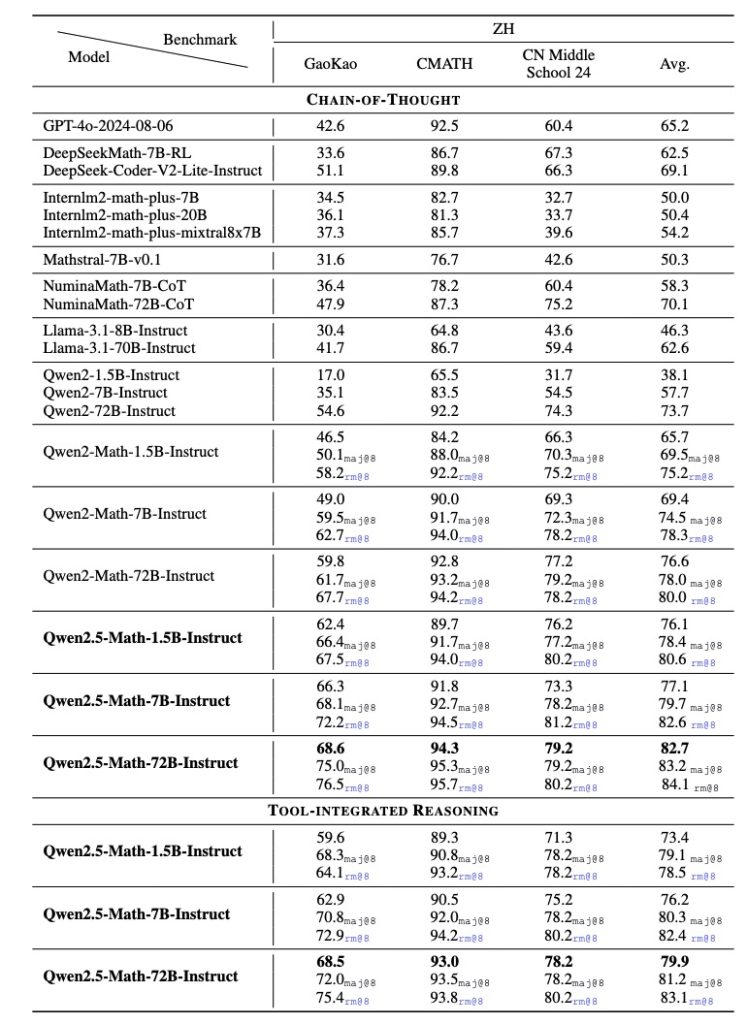
It even surpassed some well-known closed-source models on challenging exams like AIME (American Invitational Math Exam): in one comparison, while other AI models could only solve 1–2 out of 30 AIME problems, Qwen2.5-Math-72B solved 9 in a standard setting and up to 12 when using tool assistance.

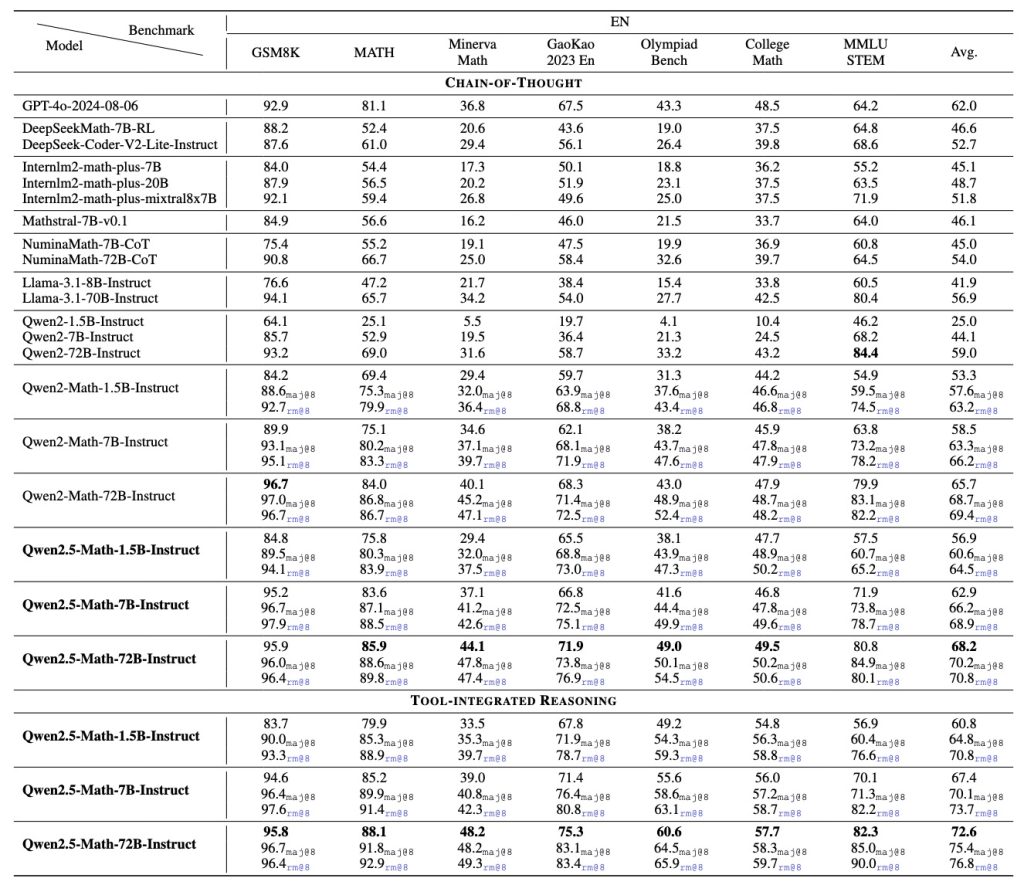
This represents a huge leap in capability for automated math reasoning. Stability-wise, the model’s chain-of-thought approach means it is more consistent in its reasoning – if you run it multiple times with temperature 0, you’re likely to get the same step-by-step solution each time, which is valuable for reproducibility in scientific contexts.

However, no model is perfect, and it’s important to understand edge cases and limitations. Accuracy on extremely complex or novel problems (especially ones that go beyond typical contest math into research-level math) may drop. The model has not necessarily seen graduate-level mathematics or highly specialized topics during training, so it might struggle or produce incorrect reasoning in those domains. Also, if a problem requires extensive computation (say a very large number multiplication or exhaustive search), Qwen2.5-Math might time out or stall in a free-form response. The tool mode can mitigate this by handing off to an actual computation, but that requires hooking the model into a runtime environment.

Another edge case to consider is logical puzzles or trick questions – if a problem is more about logic than math, or has a deceptive phrasing, the model might misinterpret it because it leans towards mathematical formalism. In terms of stability, while the model is generally deterministic with fixed seed, very long reasoning chains (hundreds of tokens of reasoning) can occasionally veer off if the model loses track of the goal. Developers might need to enforce intermediate checks (e.g. asking the model to summarize progress after a long derivation) for very lengthy problems to keep it on track.

There’s also the consideration of format consistency: if the model is instructed to give an answer in a specific format (say JSON or just a number), it usually does, but on rare occasions it might still include a sentence or some latex markup around it. Using the structured output enforcement helps, but it’s something to test for your particular use. When integrating Qwen2.5-Math into user-facing applications, one should implement validation of the output. For example, if expecting a JSON, use a JSON parser and handle errors (maybe by retrying with a stricter prompt if parsing fails). If expecting a numeric answer, you could post-process the text to extract the number.

In summary, Qwen2.5-Math’s accuracy on known benchmarks is excellent – making it suitable for serious mathematical tasks – but developers should remain mindful of the complex cases that could still trip it up. The combination of chain-of-thought and tool integration offers a new level of reliability, yet also introduces complexities (like needing an execution backend for full benefits). Through careful prompt management and output validation, these considerations can be managed, allowing the model to be a robust component in a larger system.

Limitations and Operational Notes

While Qwen2.5-Math is a powerful model for mathematical reasoning, it comes with certain limitations and operational caveats that developers should keep in mind:

Domain Specialization: As emphasized earlier, Qwen2.5-Math is not a general-purpose model. Its knowledge and optimization are heavily skewed towards math problems. If you try to use it for open-domain conversations or other tasks (like general Q&A, coding help, etc.), you may get subpar results. The model might also produce unnecessarily formal or math-styled answers even for simple questions. Therefore, use it for math (and math-related science) tasks; for other domains, consider using the general Qwen2.5 or other models.

Resource Intensity: The largest 72B model is resource-hungry – requiring multi-GPU setups (e.g. 2×80GB A100s, or 8×24GB GPUs in 16-bit precision). Even the 7B model, while much lighter, benefits from a GPU for reasonable inference speed. Running these models on CPU is possible but extremely slow (especially if generating long step-by-step solutions). If you don’t have the hardware, using the hosted API or a smaller quantized version is recommended. Also, the initial loading of the model can be time-consuming (and for 72B, you need to ensure your environment supports large model loading, possibly with DeepSpeed or other optimizations).

Latency vs. Accuracy Trade-off: With chain-of-thought, the model’s answers are longer (since it’s showing steps). This means higher latency for a single query, as compared to a model that just outputs a concise answer. In interactive settings, you might need to balance this. Qwen2.5-Math does support streaming output (the API allows streaming tokens), so you can start rendering the solution as it’s generated, which improves the user experience in a UI context. But in batch processing systems, be aware that a single query could produce a few hundred tokens of explanation, which takes longer to generate. If latency is critical, you can prompt for a brief answer or use the base model (which might output less explanation by default).

Tool Integration Requirements: The Tool-Integrated Reasoning (TIR) feature is a double-edged sword. On one hand, it yields higher accuracy by doing computations. On the other hand, to fully utilize it, you need an execution layer. The model might output some special format or code that needs to be caught and executed. Out-of-the-box, if you use the instruct model without any tool executor, it will simply describe a calculation or suggest a code. It won’t magically run Python by itself (unless you wire it up with something like a middleware that detects code blocks and runs them). The authors mention using a “Python Interpreter” to get the best score with the 1.5B model – this implies that hooking the model to an actual interpreter can significantly boost performance on certain tasks. In practical terms, if you’re building a system for say, solving user-submitted math problems, you might incorporate a step where any code emitted by the model (e.g. in a markdown block) is executed and the output is fed back into the model. This requires careful sandboxing and trust (to avoid arbitrary code execution issues). If you can’t implement such a loop, the model will still perform well with pure CoT, just not quite as perfectly on the hardest tasks.

Quality of Reasoning vs. Final Answer: Sometimes, Qwen2.5-Math’s intermediate reasoning might contain minor mistakes or unnecessary steps, even if the final answer is correct. This is a common trait with CoT-based LLMs – the “thought” is not guaranteed to be 100% logically rigorous by human standards, even if it arrives at the correct result. For use cases like generating textbook solutions or proof writing, it’s usually fine (and you might even manually edit the solution for clarity). But if you need a formal proof with absolute rigor, be prepared to review the output. The model’s strength is producing a plausible and mostly correct reasoning chain quickly, not delivering a formally verified proof.

Maintenance and Updates: As with any model, keep an eye on updates. Qwen2.5-Math was released in 2024, and it’s possible that newer versions or patches could come (e.g., Qwen3-Math in the future). Given it’s open source, the community might also fine-tune or extend it. Ensure you’re using the latest checkpoints and follow the official repository for any bug fixes (for example, initial releases of Qwen models had some quirks in the tokenizer integration which got ironed out in transformers updates).

Operationally, when deploying Qwen2.5-Math in a production system, treat it as you would a specialized math library or engine: monitor its outputs for correctness, have fallbacks for extremely tricky queries (perhaps even a symbolic math engine like SymPy as a secondary check for certain types of problems), and continuously evaluate it on your specific task distribution. With these considerations addressed, Qwen2.5-Math can be a highly effective component for enabling advanced math capabilities in your applications.

Developer-Focused FAQs

In conclusion, Qwen2.5-Math is a powerful math-oriented AI that brings advanced symbolic reasoning to the hands of developers.

With its combination of chain-of-thought reasoning, tool integration, and format-friendly outputs (LaTeX/JSON), it is well-suited for building next-generation STEM applications – from automated theorem solvers and calculus tutors to backend services that require robust math problem solving.

By understanding its architecture, capabilities, and proper use, one can harness this model to tackle complex mathematical challenges that were previously out of reach for AI systems.

The examples and guidelines above should serve as a solid foundation for utilizing Qwen2.5-Math effectively in your projects.